CBSE Class 9 Science Chapter 8 Motion Notes||सीबीएसई कक्षा 9 विज्ञान अध्याय 8 गति नोट्स

 

सीबीएसई कक्षा 9 विज्ञान अध्याय 7 गति नोट्स

कक्षा 9 विज्ञान अध्याय 8 गति में, छात्र एक सीधी रेखा के साथ वस्तुओं की गति का वर्णन करना सीखते हैं और ऐसी गति को सरल समीकरणों और ग्राफ़ के माध्यम से व्यक्त करना सीखते हैं। अध्याय में वृत्ताकार गति का वर्णन करने के तरीकों पर भी चर्चा की गई है।

अध्याय सारांश वीडियो

गति को समझना

संदर्भ बिंदु और संदर्भ फ़्रेम

• किसी वस्तु की स्थिति का वर्णन करने के लिए हमें एक संदर्भ बिंदु या मूल बिंदु की आवश्यकता होती है। एक वस्तु एक पर्यवेक्षक को गतिमान और दूसरे को स्थिर प्रतीत हो सकती है।
• उदाहरण: बस के अंदर एक यात्री देखता है कि अन्य यात्री आराम कर रहे हैं, जबकि बस के बाहर एक पर्यवेक्षक देखता है कि यात्री गति में हैं।
• अवलोकन को आसान बनाने के लिए, एक सम्मेलन या एक सामान्य संदर्भ बिंदु या फ्रेम की आवश्यकता होती है। सभी ऑब्जेक्ट एक ही संदर्भ फ़्रेम में होने चाहिए.

मोशन पर अधिक जानकारी के लिए नीचे दिए गए वीडियो देखें

दूरी एवं विस्थापन

किसी गतिशील वस्तु द्वारा तय की गई लंबाई के परिमाण को दूरी कहा जाता है। इसकी कोई दिशा नहीं है.

विस्थापन दो बिंदुओं के बीच की सबसे छोटी दूरी या समय के संबंध में प्रारंभिक और अंतिम स्थिति के बीच की दूरी है। इसमें दिशा के साथ-साथ परिमाण भी है।

विस्थापन शून्य हो सकता है, लेकिन दूरी नहीं।

दूरी बनाम विस्थापन

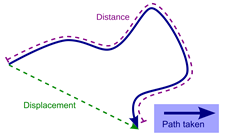
दूरी और विस्थापन के बारे में अधिक जानने के लिए यहां जाएं ।

परिमाण

परिमाण किसी भौतिक राशि का आकार या विस्तार है। भौतिकी में, हमारे पास अदिश और सदिश राशियाँ हैं।

अदिश राशियाँ केवल परिमाण के रूप में व्यक्त की जाती हैं। जैसे: समय, दूरी, द्रव्यमान, तापमान, क्षेत्रफल, आयतन

सदिश राशियाँ परिमाण के साथ-साथ वस्तु की दिशा में भी व्यक्त की जाती हैं। जैसे: वेग, विस्थापन, भार, संवेग, बल, त्वरण, आदि।

समय, औसत गति और वेग

समय और गति

समय किसी घटना की अवधि है जिसे सेकंड में व्यक्त किया जाता है। अधिकांश भौतिक घटनाएँ समय के सापेक्ष घटित होती हैं। यह एक अदिश राशि है.

गति दूरी में परिवर्तन की दर है। यदि कोई पिंड एक निश्चित समय में एक निश्चित दूरी तय करता है, तो उसकी गति दी जाती है

$\begin{array}{l}गति=\frac{दूरी}{समय}\end{array}$

तात्कालिक गति समय में किसी विशेष क्षण में किसी वस्तु की गति है।

औसत गति को किसी समयावधि के भीतर वस्तु द्वारा तय की गई दूरी के रूप में बताया जाता है।

औसत गति = तय की गई कुल दूरी / लिया गया कुल समय

नीचे दी गई तालिका औसत गति और तात्कालिक गति के बीच अंतर को सूचीबद्ध करती है।

औसत गति	तत्काल गति
इसे तय की गई कुल दूरी को बीते हुए कुल समय से विभाजित करके परिभाषित किया जाता है।	इसे समय के एक विशेष क्षण में गति के रूप में परिभाषित किया गया है।
यह स्थिर है.	यह स्थिर नहीं है.
संपूर्ण यात्रा की गति की गणना करके मापा जाता है।	इसे स्पीडोमीटर से मापा जाता है.
उदाहरण: एक कार 60 किमी प्रति घंटे की गति से यात्रा कर रही है। इस प्रकार, कार की औसत गति 60 किमी प्रति घंटा है।	उदाहरण: एक कार एक निश्चित समय पर एक निश्चित गति से यात्रा कर रही है जिसे स्पीडोमीटर द्वारा दिया जा सकता है।

एकसमान गति और गैर-समान गति

जब कोई वस्तु समान समय अंतराल में समान दूरी तय करती है, तो वह एकसमान गति में होती है।

एकसमान गति के उदाहरण

• छत के पंखे के ब्लेड का हिलना।
• सूर्य के चारों ओर पृथ्वी की गति
• दोनों तरफ समान आयाम वाला पेंडुलम

जब कोई वस्तु समान समय अंतराल में असमान दूरी तय करती है, तो उसे असमान गति में कहा जाता है।

• उछलती गेंद
• दौड़ता हुआ घोड़ा
• चलती ट्रेन

यूनिफ़ॉर्म मोशन और नॉन-यूनिफ़ॉर्म मोशन के बारे में अधिक जानने के लिए, यहां जाएँ ।

वेग

विस्थापन परिवर्तन की दर वेग है। यह एक सदिश राशि है. यहां गति की दिशा निर्दिष्ट है।

$\begin{array}{l}वेग=\frac{विस्थापन}{समय}\end{array}$

तात्क्षणिक वेग एक समय अंतराल के लिए स्थिति परिवर्तन की दर है जो बहुत छोटी अर्थात लगभग शून्य होती है। अधिक सरल शब्दों में, किसी निश्चित समय पर किसी वस्तु के वेग को तात्क्षणिक वेग कहा जाता है।

औसत वेग को विस्थापन (∆x) के रूप में परिभाषित किया जाता है जिसे उस समय अंतराल (∆t) से विभाजित किया जाता है जिसमें विस्थापन होता है।

$\begin{array}{l}औसतवेग=\frac{प्रारंभिकवेग+अंतिमवेग}{2}\end{array}$

औसत वेग	तात्कालिक वेग
औसत वेग को विस्थापन (∆x) के रूप में परिभाषित किया जाता है जिसे उस समय अंतराल (∆t) से विभाजित किया जाता है जिसमें विस्थापन होता है।	तात्क्षणिक वेग एक समय अंतराल के लिए स्थिति परिवर्तन की दर है जो बहुत छोटी अर्थात लगभग शून्य होती है।
औसत वेग की गणना विस्थापन की दर को बीते समय से विभाजित करके की जाती है।	तात्कालिक वेग की गणना उस क्षण में विस्थापन को समय से विभाजित करके की जाती है।
यदि जैक को अपने घर से स्कूल तक 10 किमी की यात्रा करने में कुल 1 घंटा लगता है, तो उसका औसत वेग 10 किमी/घंटा होगा।	जैक के मामले में, स्कूल जाते समय, जब वह बैठा है और ट्रेन गुजरने का इंतजार कर रहा है, तो उसका तात्कालिक वेग शून्य होगा। यद्यपि यात्रा के एक छोटे से भाग के लिए तात्कालिक वेग शून्य था, औसत वेग शून्य नहीं होगा।

औसत गति और वेग के बारे में अधिक जानकारी के लिए नीचे दिया गया वीडियो देखें

औसत गति और औसत वेग के बारे में अधिक जानने के लिए यहां जाएं ।

त्वरण

वेग में परिवर्तन की दर को त्वरण कहते हैं। यह एक सदिश राशि है. गैर-समान गति में, वेग समय के साथ बदलता रहता है, अर्थात, वेग में परिवर्तन 0 नहीं होता है। इसे "ए" द्वारा दर्शाया जाता है।

$Acceleration=$ वेग/समय में परिवर्तन

(या)

$\begin{array}{l}�=\frac{��}{�}\end{array}$

जहां t (लिया गया समय), v (अंतिम वेग) और u (प्रारंभिक वेग)।

एक्सेलेरेशन के बारे में अधिक जानने के लिए यहां जाएं ।

मोशन विज़ुअलाइज़्ड

दूरी-समय ग्राफ

• दूरी-समय ग्राफ़ समय के सापेक्ष किसी वस्तु की स्थिति में परिवर्तन को दर्शाता है।
• रैखिक भिन्नता = एकसमान गति और गैर-रेखीय विविधताएं गैर-समान गति दर्शाती हैं
• ढलान हमें गति प्रदान करती है

दूरी - समय ग्राफ़

• OA का तात्पर्य स्थिर गति के साथ एकसमान गति से है क्योंकि ढलान स्थिर है
• एबी का तात्पर्य है कि शरीर आराम की स्थिति में है क्योंकि ढलान शून्य है
• B से C एक गैर-समान गति है

दूरी-समय ग्राफ़ के बारे में अधिक जानने के लिए, यहां जाएँ ।

वेग-समय ग्राफ

• वेग-समय ग्राफ़ समय के संबंध में वेग में परिवर्तन दिखाते हैं।
• ढलान त्वरण देता है
• वक्र के नीचे का क्षेत्र विस्थापन देता है
• x-अक्ष के समांतर रेखा स्थिर वेग को दर्शाती है-

वेग - समय ग्राफ

OA = स्थिर त्वरण, AB = स्थिर वेग, BC = स्थिर मंदता

वेग-समय ग्राफ़ के बारे में अधिक जानने के लिए, यहां जाएँ ।

गति के समीकरण

एकसमान त्वरण से गतिमान किसी वस्तु की गति को तीन समीकरणों की सहायता से वर्णित किया जा सकता है, अर्थात्

(i) v = u + at

(ii) v 2 - u 2 = 2as

(iii) s = ut + (1/2) 2 पर

जहाँ u प्रारंभिक वेग है, v अंतिम वेग है, t समय है, a त्वरण है और s विस्थापन है।

गति के समीकरणों के बारे में अधिक जानने के लिए, यहां जाएँ ।

ग्राफिकल विधि द्वारा वेग-समय संबंध की व्युत्पत्ति

वेग - समय ग्राफ

एक पिंड A पर कुछ प्रारंभिक गैर-शून्य वेग से शुरू होता है और निरंतर त्वरण a के साथ B तक जाता है।

ग्राफ़ से BD = v (अंतिम वेग) – DC = u (प्रारंभिक वेग)…………..(eq 1)।

बीडी = बीसी - डीसी…………..( ईक 2 )।

$\text{Missing end{array}}$

.

  BD = ……………….(eq 3) पर।

हमें जो कुछ भी मिलता है उसे प्रतिस्थापित करें: at = v – u.

v = u + at प्राप्त करने के लिए पुनर्व्यवस्थित करें।

आलेखीय विधि द्वारा स्थिति-समय संबंध की व्युत्पत्ति

वेग - समय ग्राफ

एक पिंड A पर कुछ प्रारंभिक गैर-शून्य वेग से शुरू होता है और निरंतर त्वरण a के साथ B तक जाता है

ग्राफ़ के अंतर्गत क्षेत्रफल इस प्रकार विस्थापन देता है:

$\text{Missing end{array}}$

OA = u , OC = t और BD = at

(eq 1) में प्रतिस्थापित करने पर हमें $s=\; प्राप्त\; होता\; है$

$\begin{array}{l}��+\frac{1}{2}�{�}^2\end{array}$

आलेखीय विधि द्वारा स्थिति-वेग संबंध की व्युत्पत्ति

वेग - समय ग्राफ

एक पिंड A पर कुछ प्रारंभिक गैर-शून्य वेग से शुरू होता है और निरंतर त्वरण a के साथ B तक जाता है

विस्थापन में वक्र के नीचे का क्षेत्र शामिल होगा जो समलंब OABC है।

हम जानते हैं कि समलम्ब चतुर्भुज का क्षेत्रफल है 

$\begin{array}{l}�=\frac{(��+��)}{2\ast ��}\end{array}$

OA = u और BC = v और OC = t

$\begin{array}{l}इसलिए,�=\frac{(�+�)}{2\ast �}\dots \dots \dots \dots \dots (��1)\end{array}$

$\begin{array}{l}हमयहभीजानतेहैंकि�=\frac{(��)}{�}\dots \dots \dots \dots \dots ..(��2)\end{array}$

(eq 1) में (eq 2) रखें और प्राप्त करने की व्यवस्था करें

v 2 −u 2 =2as

एकसमान वृत्तीय गति

एकसमान वृत्तीय गति

• यदि कोई वस्तु वृत्ताकार पथ पर एकसमान गति से चलती है तो उसकी गति को एकसमान वृत्तीय गति कहा जाता है।
• जैसे-जैसे दिशा बदलती रहती है, वेग भी बदलता रहता है।
• त्वरण स्थिर है.
• एकसमान वृत्ताकार वेग निम्नलिखित सूत्र द्वारा दिया गया है:
  $\begin{array}{l}�=\frac{2�}{�}\end{array}$

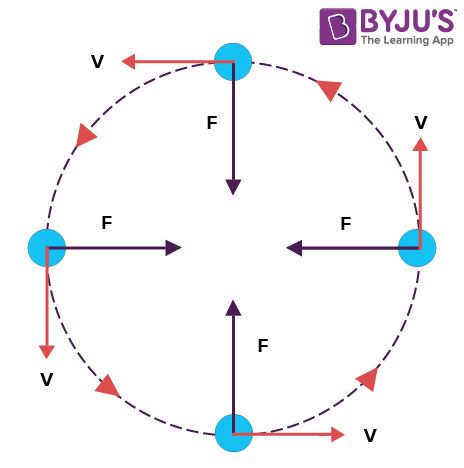
एकसमान वृत्ताकार गति के उदाहरण

• पृथ्वी के चारों ओर कृत्रिम उपग्रहों की गति एकसमान वृत्तीय गति का उदाहरण है।
• इसके नाभिक के चारों ओर इलेक्ट्रॉनों की गति।
• पवन चक्कियों के ब्लेडों की गति.
• गोलाकार डायल वाली घड़ी की दूसरी सुई की नोक एकसमान गोलाकार गति दर्शाती है।

यूनिफ़ॉर्म सर्कुलर मोशन के बारे में अधिक जानने के लिए यहां जाएं ।